一,定义
1.1 锐角三角函数
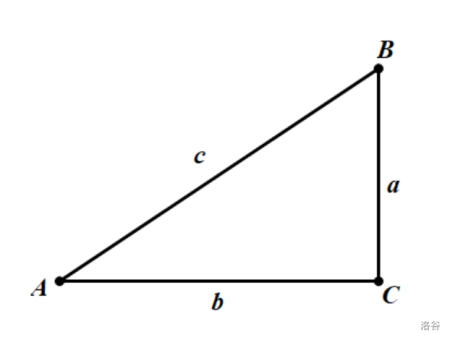
如图,在 \({\rm Rt}\triangle ABC\) 中,\(\angle C=90^{\circ}\) ,则有:
-
\(\sin A=\dfrac ac\) (正弦值等于对边比斜边)
-
\(\cos A=\dfrac bc\) (余弦值等于邻边比斜边)
-
\(\tan A=\dfrac ab\) (正切值等于对边比邻边)
-
\(\cot A=\dfrac ba\) (余切值等于邻边比对边)
-
\(\sec A=\dfrac cb\) (正割值等于斜边比邻边)
-
\(\csc A=\dfrac ca\) (余割值等于斜边比对边)
中学阶段最常用的是 \(\sin,\cos,\tan,\cot\)
下文将不再讨论 \(\sec,\csc\) 及其他三角函数
1.2 任意角三角函数
构造平面直角坐标系 \(xOy\)
将 \(x\) 轴正半轴绕点 \(O\) 逆时针旋转一个角度 \(\theta\) 得到射线 \(l\)
设 \(P(x,y)\) 为 \(l\) 上一点,\(OP=r\) ,则有:
-
\(\sin\theta=\dfrac yr\)
-
\(\cos\theta=\dfrac xr\)
-
\(\tan\theta=\dfrac yx\)
-
\(\cot\theta=\dfrac xy\)
下图是 \(\alpha\in(\frac{\pi}2,\pi)\) 的情况
\(P\) 点在单位圆上,坐标为 \((\cos \alpha,\sin\alpha)\)
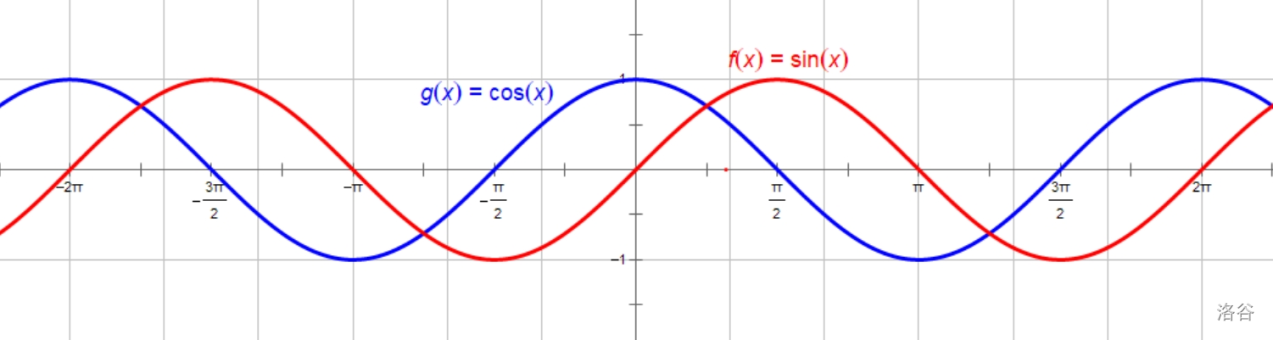
\(\sin\) 和 \(\cos\) 的函数图象如下图所示
1.3 反三角函数
反三角函数指三角函数的反函数,用 arc + 函数名 的形式表示
如 \(\arctan\dfrac ab\) 表示满足 \(\tan\theta=\dfrac ab\) 的 \(\theta\) 值
\(\arctan\) 的值域(主值区间)为 \((-\frac\pi 2,\frac\pi 2)\) ,这是为了保证一个自变量恰好对应一个函数值,同时方便使用
例如 3.7 中的辅助角公式使用不当容易出错,而直接用 \(\arctan\) 不会有问题,其实就和它的值域定义有关
\(\arcsin,\arccos,\operatorname{arccot}\) 的值域可参考 2.1 中表格
二,基本性质
2.1 定义域 & 值域
| 三角函数 | 定义域 |
值域 | 反三角函数 | 定义域 | 值域(主值区间) |
|---|---|---|---|---|---|
| \(\sin\) | \(\mathbb R\) | \([-1,1]\) | \(\arcsin\) | \([-1,1]\) | \([-\frac\pi 2,\frac\pi 2]\) |
| \(\cos\) | \(\mathbb R\) | \([-1,1]\) | \(\arccos\) | \([-1,1]\) | \([0,\pi]\) |
| \(\tan\) | \(\{x\mid x\ne k\pi+\frac\pi 2(k\in \mathbb Z)\}\) | \(\mathbb R\) | \(\arctan\) | \(\mathbb R\) | \((-\frac\pi 2,\frac\pi 2)\) |
| \(\cot\) | \(\{x\mid x\ne k\pi(k\in \mathbb Z)\}\) | \(\mathbb R\) | \(\operatorname{arccot}\) | \(\mathbb R\) | \((0,\pi)\) |
2.2 奇偶性 & 单调性 & 周期性
| 三角函数 | 奇偶性 | 最小正周期 | 反三角函数 | 奇偶性 | 单调性 |
|---|---|---|---|---|---|
| \(\sin\) | 奇 | \(2\pi\) | \(\arcsin\) | 奇 | 单调递增 |
| \(\cos\) | 偶 | \(2\pi\) | \(\arccos\) | 非奇非偶 | 单调递减 |
| \(\tan\) | 奇 | \(\pi\) | \(\arctan\) | 奇 | 单调递增 |
| \(\cot\) | 奇 | \(\pi\) | \(\operatorname{arccot}\) | 非奇非偶 | 单调递减 |
\(\sin,\cos,\tan,\cot\) 的单调性略
\(\arcsin,\arccos,\arctan,\operatorname{arccot}\) 都不是周期函数
2.3 对称性
咕咕咕
自己画图看吧(
2.4 特殊值
| \(\theta\rm(deg)\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\theta\rm(rad)\) | \(0\) | \(\dfrac\pi6\) | \(\dfrac\pi4\) | \(\dfrac\pi3\) | \(\dfrac\pi2\) | \(\dfrac{2\pi}3\) | \(\dfrac{3\pi}4\) | \(\dfrac{5\pi}6\) | \(\pi\) |
| \(\sin\theta\) | \(0\) | \(\dfrac12\) | \(\dfrac{\sqrt2}2\) | \(\dfrac{\sqrt3}2\) | \(1\) | \(\dfrac{\sqrt3}2\) | \(\dfrac{\sqrt2}2\) | \(\dfrac12\) | \(0\) |
| \(\cos\theta\) | \(1\) | \(\dfrac{\sqrt3}2\) | \(\dfrac{\sqrt2}2\) | \(\dfrac12\) | \(0\) | \(-\dfrac12\) | \(-\dfrac{\sqrt2}2\) | \(-\dfrac{\sqrt3}2\) | \(-1\) |
| \(\tan\theta\) | \(0\) | \(\dfrac{\sqrt3}3\) | \(1\) | \(\sqrt3\) | \(\backslash\) | \(-\sqrt3\) | \(-1\) | \(-\dfrac{\sqrt3}3\) | \(0\) |
| \(\cot\theta\) | \(\backslash\) | \(\sqrt3\) | \(1\) | \(\dfrac{\sqrt3}3\) | \(0\) | \(-\dfrac{\sqrt3}3\) | \(-1\) | \(-\sqrt3\) | \(\backslash\) |
\(15^{\circ}\) 和 \(75^{\circ}\) 的三角函数值也有可能会用到:
\(\sin15^{\circ}=\dfrac{\sqrt6-\sqrt2}4,~~\cos15^{\circ}=\dfrac{\sqrt6+\sqrt2}4,~~\tan15^{\circ}=2-\sqrt3,~~\cot15^{\circ}=2+\sqrt3\)
\(\sin75^{\circ}=\dfrac{\sqrt6+\sqrt2}4,~~\cos75^{\circ}=\dfrac{\sqrt6-\sqrt2}4,~~\tan75^{\circ}=2+\sqrt3,~~\cot75^{\circ}=2-\sqrt3\)
2.5 基本关系式
-
\(\sin^2\theta+\cos^2\theta=1\)
-
\(\tan\theta=\dfrac{\sin\theta}{\cos\theta},~~\cot\theta=\dfrac{\cos\theta}{\sin\theta}\)
-
\(\tan\theta\cot\theta=1\)
-
\(\sin\theta=\cos(90^{\circ}-\theta),~~\tan\theta=\cot(90^{\circ}-\theta)\)
都是初中知识 证明略
三,三角恒等变形
3.1 诱导公式
诱导公式的作用是将 \(n\cdot\dfrac\pi2\pm \alpha\) 这种角的三角函数转化为 \(\alpha\) 的三角函数
首先,根据三角函数的周期性,对于 \(\theta=2k\pi+\alpha(k\in\mathbb Z)\) ,有
\(\begin{aligned} \sin(2k\pi+\alpha)&=\sin\alpha\\ \cos(2k\pi+\alpha)&=\cos\alpha\\ \tan(2k\pi+\alpha)&=\tan\alpha\\ \cot(2k\pi+\alpha)&=\cot\alpha \end{aligned}\)
诱导公式的其它部分如下表所示
| \(\theta\rm(deg)\) | \(-\alpha\) |
\(90^{\circ}-\alpha\) |
\(90^{\circ}+\alpha\) |
\(180^{\circ}-\alpha\) |
\(180^{\circ}+\alpha\) |
\(270^{\circ}-\alpha\) |
\(270^{\circ}+\alpha\) |
\(360^{\circ}-\alpha\) |
|---|---|---|---|---|---|---|---|---|
| \(\theta\rm(rad)\) | \(-\alpha\) | \(\dfrac\pi2-\alpha\) | \(\dfrac\pi2+\alpha\) | \(\pi-\alpha\) | \(\pi+\alpha\) | \(\dfrac{3\pi}2-\alpha\) | \(\dfrac{3\pi}2+\alpha\) | \(2\pi-\alpha\) |
| \(\sin\theta\) | \(-\sin\alpha\) | \(\cos\alpha\) | \(\cos\alpha\) | \(\sin\alpha\) | \(-\sin\alpha\) | \(-\cos\alpha\) | \(-\cos\alpha\) | \(-\sin\alpha\) |
| \(\cos\theta\) | \(\cos\alpha\) | \(\sin\alpha\) | \(-\sin\alpha\) | \(-\cos\alpha\) | \(-\cos\alpha\) | \(-\sin\alpha\) | \(\sin\alpha\) | \(\cos\alpha\) |
| \(\tan\theta\) | \(-\tan\alpha\) | \(\cot\alpha\) | \(-\cot\alpha\) | \(-\tan\alpha\) | \(\tan\alpha\) | \(\cot\alpha\) | \(-\cot\alpha\) | \(-\tan\alpha\) |
| \(\cot\theta\) | \(-\cot\alpha\) | \(\tan\alpha\) | \(-\tan\alpha\) | \(-\cot\alpha\) | \(\cot\alpha\) | \(\tan\alpha\) | \(-\tan\alpha\) | \(-\cot\alpha\) |
证明全部都可以直接套定义得到,但还是建议结合函数图象的性质理解记忆
3.2 和差角公式
\(\begin{aligned} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ \sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\ \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ \cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\ \tan(\alpha+\beta)&=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\ \tan(\alpha-\beta)&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{aligned}\)
证明思路:
前四个中只需任意证明一个,再结合诱导公式即可得出另外三个
然后一三式、二四式分别相除即可得到五、六式
例如 \(\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
分子分母同时约去 \(\cos\alpha\cos\beta\) 即可得到 \(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)
下面给出两种证明方法(在三角形内证明一式、向量法证明四式)
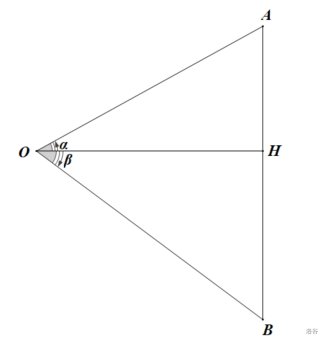
以 \(\alpha,\beta\) 均为锐角的情形为例
\(S_{\triangle AOH}=\dfrac12OA\cdot OH\cdot \sin\alpha=\dfrac12OA\cdot OB\cdot\cos\beta\cdot\sin\alpha\)
\(S_{\triangle BOH}=\dfrac12OB\cdot OH\cdot \sin\beta=\dfrac12OB\cdot OA\cdot\cos\alpha\cdot\sin\beta\)
\(S_{\triangle AOB}=\dfrac12OA\cdot OB\cdot \sin(\alpha+\beta)\)
显然 \(S_{\triangle AOB}=S_{\triangle AOH}+S_{\triangle BOH}\) ,故 \(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\) ,即为一式
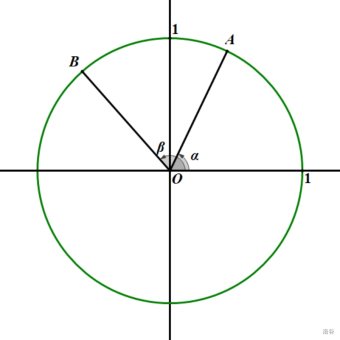
\(A,B\) 都在单位圆上,故 \(A,B\) 的坐标分别为 \((\cos\alpha,\sin\alpha),(\cos\beta,\sin\beta)\)
考虑向量 \(\overrightarrow{OA},\overrightarrow{OB}\) 的数量积
根据定义, \(\overrightarrow{OA}\cdot\overrightarrow{OB}=|OA|\cdot|OB|\cdot\cos(\beta-\alpha)=\cos(\beta-\alpha)=\cos(\alpha-\beta)\)
再考虑数量积的坐标表示,有 \(\overrightarrow{OA}\cdot\overrightarrow{OB}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
故 \(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\) ,即为四式
3.3 倍角公式
在和角公式中令 \(\alpha=\beta\) ,即可得到二倍角公式:
\(\begin{aligned} \sin2\alpha&=2\sin\alpha\cos\alpha\\ \cos2\alpha&=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha\\ \tan2\alpha&=\dfrac{2\tan\alpha}{1-\tan^2\alpha} \end{aligned}\)
由二倍角公式可得 \(\cos\alpha=2\cos^2\dfrac\alpha2-1=1-2\sin^2\dfrac\alpha2\)
进一步可以推出半角公式:
\(\begin{aligned} \sin\dfrac\alpha2&=\pm\sqrt{\dfrac{1-\cos\alpha}2}\\ \cos\dfrac\alpha2&=\pm\sqrt{\dfrac{1+\cos\alpha}2}\\ \tan\dfrac\alpha2&=\pm\sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}}=\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha} \end{aligned}\)
带 \(\pm\) 是因为开方导致符号不确定,还需要根据 \(\dfrac\alpha2\) 所在的象限判断
但 \(\tan\dfrac\alpha2=\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha}\) 是没有符号问题的 可以直接用
三倍角公式偶尔也会用到 放到后面再讲
四倍及以上就没必要记了
3.4 万能公式
功能是仅用 \(\tan\dfrac\alpha2\) 表示出 \(\alpha\) 的三角函数值
首先根据二倍角公式有
\(\begin{aligned} \sin\alpha&=2\sin\dfrac\alpha2\cos\dfrac\alpha2\\ \cos\alpha&=\cos^2\dfrac\alpha2-\sin^2\dfrac\alpha2\\ \tan\alpha&=\dfrac{2\tan\frac\alpha2}{1-\tan^2\frac\alpha2} \end{aligned}\)
三式已经达成目标了
因为 \(1=\sin^2\frac\alpha2+\cos^2\frac\alpha2\) ,所以我们可以把一二式写成
\(\sin\alpha=\dfrac{2\sin\frac\alpha2\cos\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2}, \cos\alpha=\dfrac{\cos^2\frac\alpha2-\sin^2\frac\alpha2}{\sin^2\frac\alpha2+\cos^2\frac\alpha2}\)
然后就可以约分了,最终得到
\(\begin{aligned} \sin\alpha&=\dfrac{2\tan\frac\alpha2}{1+\tan^2\frac\alpha2}\\ \cos\alpha&=\dfrac{1-\tan^2\frac\alpha2}{1+\tan^2\frac\alpha2}\\ \tan\alpha&=\dfrac{2\tan\frac\alpha2}{1-\tan^2\frac\alpha2} \end{aligned}\)
即为万能公式
3.5 积化和差公式
根据和差角公式,\(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)
两式相加,两式相减,分别可得出
\(\begin{aligned} \cos\alpha\cos\beta&=\dfrac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)]\\ \sin\alpha\sin\beta&=\dfrac12[\cos(\alpha-\beta)-\cos(\alpha+\beta)] \end{aligned}\)
同理,由 \(\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\) 可得
\(\begin{aligned} \sin\alpha\cos\beta&=\dfrac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\ \cos\alpha\sin\beta&=\dfrac12[\sin(\alpha+\beta)-\sin(\alpha+\beta)] \end{aligned}\)
这四个式子就是积化和差公式
\(\begin{aligned} \sin\alpha\sin\beta&=-\dfrac12[\cos(\alpha+\beta)-\cos(\alpha-\beta)]\\ \sin\alpha\cos\beta&=\dfrac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\ \cos\alpha\sin\beta&=\dfrac12[\sin(\alpha+\beta)-\sin(\alpha-\beta)]\\ \cos\alpha\cos\beta&=\dfrac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)] \end{aligned}\)
3.6 和差化积公式
\(\begin{aligned} \sin\alpha+\sin\beta&=2\sin\tfrac{\alpha+\beta}2\cos\tfrac{\alpha-\beta}2\\ \sin\alpha-\sin\beta&=2\cos\tfrac{\alpha+\beta}2\sin\tfrac{\alpha-\beta}2\\ \cos\alpha+\cos\beta&=2\cos\tfrac{\alpha+\beta}2\cos\tfrac{\alpha-\beta}2\\ \cos\alpha-\cos\beta&=-2\sin\tfrac{\alpha+\beta}2\sin\tfrac{\alpha-\beta}2 \end{aligned}\)
证明不写了,用积化和差从右往左推就行
3.7 其它公式
三倍角公式
一种证法是对二倍角和一倍角用一次和角公式
也可以用复数运算来推,将 \((\cos\alpha+i\sin\alpha)^3=\cos3\alpha+i\sin3\alpha\) 的左边展开,整理化简即可
\(\begin{aligned} \sin3\alpha&=3\sin\alpha-4\sin^3\alpha=4\sin(60^{\circ}-\alpha)\sin\alpha\sin(60^{\circ}+\alpha) \\ \cos3\alpha&=4\cos^3\alpha-3\cos\alpha=4\cos(60^{\circ}-\alpha)\cos\alpha\cos(60^{\circ}+\alpha) \\ \tan3\alpha&=\dfrac{\tan^3\alpha-3\tan\alpha}{3\tan^2\alpha-1}=\tan(60^{\circ}-\alpha)\tan\alpha\tan(60^{\circ}+\alpha) \end{aligned}\)
辅助角公式
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\arctan\frac ba)\quad (a>0)\)
用和角公式把右边拆了就能证
化简函数解析式时常会用到,一般放在最后一步
说句闲话,平时似乎经常见到这种写法:
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\varphi)\) ,其中 \(\tan\varphi=\dfrac ba\)
如果这是对的,我们可以得到 \(a\sin x+b\cos x=-a\sin x-b\cos x\)
还可以得到 \(\sin(x+\varphi)=\sin(x+\varphi+\pi)\)
总之这就是瞎扯,纯属误导人的 nt 写法
平方差公式(?)
\(\sin^2\alpha-\sin^2\beta=\sin(\alpha+\beta)\sin(\alpha-\beta)\)
读者自证不难
