Jones矢量、Stokes参量、Poincare球、Bloch球

总结一下光的偏振态表示，以及Poincare球和Bloch球的相似性，以及偏振度。盗了两张示意图。部分内容是Wikipedia上面的，结合了手里有的书化简了一下，有的内容是自己推的。一开始读量子信息书的时候就对于光的偏振态的这种“量子”的表述感到好奇，粗读下来好像也不记得哪里有仔细讲过。这篇总结罗列了这些东西，其实是半年前写的，本来读的书、文章就少，已经有段时间没碰相关的东西了，再深入的思考就以后再说吧。
更新-2021-09-06：给出了偏振片透射光功率和Stokes参量的关系式的参考文献[1].

Jones矢量

考虑沿着$+z$方向传播的平面波，电场可以写为

\[\left(\begin{array}{c}{E_{x}(t)} \\ {E_{y}(t)} \\ {0}\end{array}\right)=\left(\begin{array}{c}{E_{0 x} e^{i\left(k z-\omega t+\phi_{x}\right)}} \\ {E_{0 y} e^{i\left(k z-\omega t+\phi_{y}\right)}} \\ {0}\end{array}\right)=\left(\begin{array}{c}{E_{0 x} e^{i \phi_{x}}} \\ {E_{0 y} e^{i \phi_{y}}} \\ {0}\end{array}\right) e^{i(k z-\omega t)} \]

Jones矢量取为

\[\left(\begin{array}{l}{E_{0 x} e^{i \phi_{x}}} \\ {E_{0 y} e^{i \phi_{y}}}\end{array}\right) \]

注意如果对Jones矢量归一化，则不含强度信息，只表示一个完全偏振光的偏振态。Jones矢量可以提取出来一个全局相位因子。$(1,0)^\text{T}$表示$|H\rangle$光，$(0,1)^\text{T}$表示$|V\rangle$光，之所以用归一化的列向量以及狄拉克符号来表示偏振态，是因为Jones矩阵表示的光的偏振和量子态的相似性。可以验证$(1,-i)^\text{T}/\sqrt{2}$是右旋光（光入射至眼睛，发现在空间固定一点，电场矢量逆时针转动），而$(1,i)^\text{T}/\sqrt{2}$是左旋光。

光通过偏振片、波片后，Jones向量就等于该元件的Jones矩阵乘以入射光的Jones向量。可以推导得到，一个快轴和水平方向夹角为$\theta$的四分之一波片的Jones矩阵为

\[e^{-\frac{i \pi}{4}}\left(\begin{array}{cc}{\cos ^{2} \theta+i \sin ^{2} \theta} & {(1-i) \sin \theta \cos \theta} \\ {(1-i) \sin \theta \cos \theta} & {\sin ^{2} \theta+i \cos ^{2} \theta}\end{array}\right) \]

一个快轴和水平方向夹角为$\theta$的半波片的Jones矩阵为

\[e^{-\frac{i \pi}{2}}\left(\begin{array}{cc}{\cos ^{2} \theta-\sin ^{2} \theta} & {2 \cos \theta \sin \theta} \\ {2 \cos \theta \sin \theta} & {\sin ^{2} \theta-\cos ^{2} \theta}\end{array}\right) \]

对于任意种类的偏振片的Jones矩阵，可以直接类比量子力学中的投影算符得到：设该偏振片允许通过的光的偏振由Jones矢量$|\psi\rangle$描述，则它的Jones矩阵为$|\psi\rangle\langle\psi|$，由此可以计算水平偏振片、斜45度偏振片、圆偏偏振片的Jones矩阵。注意，这些矩阵都是幺正的。

偏振椭圆

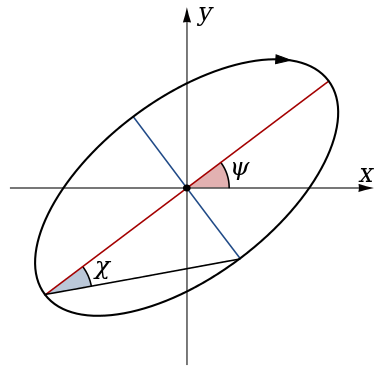
偏振椭圆的方程是容易求出的（消去参数$t$即可）

\[\left(\frac{E_x}{E_{0x}}\right)^2+\left(\frac{E_y}{E_{0y}}\right)^2-2\left(\frac{E_x}{E_{0x}}\right)\left(\frac{E_y}{E_{0y}}\right)\cos\phi=\sin^2\phi \]

其中$\phi$是相位差。如图所示，其中的两个角$\psi,\chi$描述了偏振椭圆的取向。为了简单地表达这两个角，除了相位差$\phi$以外，再引入一个范围在$[0,\pi/2]$的角$\alpha$满足$\tan \alpha=E_{0y}/E_{0x}$，有了这些就可以计算得到

\[\tan(2\psi)=\tan(2\alpha)\cos\phi \]

\[\sin(2\chi)=\sin(2\alpha)\sin\phi \]

其中，规定$0\leqslant\psi<\pi$，$-\pi/4\leqslant\chi\leqslant\pi/4$.

Stokes参量和偏振度

对于完全偏振的平面光波, 定义Stokes参量定义为$(S_0,S_1,S_2,S_3)^T$,$其中S_0=I=E_{0x}^2+E_{0y}^2$是光强, $S_1=E_{0x}^2-E_{0y}^2$, $S_2=2E_{0x}E_{0y}\cos\phi$, $S_3=2E_{0x}E_{0y}\sin\phi$, 而$\phi$是$x,y$方向振动的相位差。如果引入上面偏振椭圆里面的增设变量$\psi,\chi$, 则Stokes参量还可以表示为（Stokes参量都是实数，而Jones向量一般是复的）：

\[\begin{pmatrix} S_0\\S_1\\S_2\\S_3 \end{pmatrix}=\begin{pmatrix} I\\ I\cos2\psi\cos2\chi\\ I\sin2\psi\cos2\chi\\ I\sin2\chi \end{pmatrix} \]

另一方面, Jones矢量也可以表示出完全偏振平面光波的偏振态, 由上式可以直接看出Jones矢量$(E_x,E_y)^\text{T}$和Stokes参量之间的关系如下（注意下标的有无），

\[\begin{pmatrix} S_0\\S_1\\S_2\\S_3 \end{pmatrix}=\begin{pmatrix} |E_x|^2+|E_y|^2\\ |E_x|^2-|E_y|^2\\ 2\text{Re}[E_xE_y^*]\\ -2\text{Im}[E_xE_y^*] \end{pmatrix} \]

注意Stokes参量的四个参数并不独立, 后三个的平方和等于第一个, 因此可以除以$S_0$使得Stokes参量归一化。

上面是Stokes参量的三种表示方法。

观察第三种表示方法，对于完全偏振情形, 可以发现

\[\begin{aligned} S_1=(E_x^*,E_y^*)\begin{pmatrix}1&0\\0&-1\end{pmatrix}\begin{pmatrix}E_x\\E_y\end{pmatrix} \end{aligned}=\langle\xi|\sigma_z|\xi\rangle \]

同理, 有$S_2=U=\langle\xi|\sigma_x|\xi\rangle$和$S_3=V=\langle\xi|\sigma_y|\xi\rangle$。所以当Stokes参量和Jones矢量都归一化后, Stokes参量可写为

\[\begin{pmatrix} S_0\\S_1\\S_2\\S_3 \end{pmatrix}=\begin{pmatrix} \langle \hat{I}\rangle\\ \langle\hat{\sigma}_z\rangle\\ \langle\hat{\sigma}_x\rangle\\ \langle\hat{\sigma}_y\rangle \end{pmatrix}= \begin{pmatrix} \text{tr}( \hat{\rho}\hat{I})\\ \text{tr}( \hat{\rho}\hat{\sigma}_z)\\ \text{tr}( \hat{\rho}\hat{\sigma}_x)\\ \text{tr}( \hat{\rho}\hat{\sigma}_y) \end{pmatrix}\tag{$*$} \]

其中$\hat{\rho}=|\xi\rangle\langle\xi|$是纯态密度矩阵, 而$\hat{I}$是单位算符。

对于一束由归一化的Stokes参量$(1,{\bf{S}})^\text{T}$描述的完全偏振光, 现在求其通过某偏振片后的光强, 而该偏振片的允许偏振由归一化的Stokes参量$(1,{\bf{D}})^\text{T}$描述, 则经过计算, 通过后的光强为[1]

\[I'=\frac{1}{2} \begin{pmatrix} 1,\bf{D} \end{pmatrix}\begin{pmatrix} 1\\ {\bf{S}}^\text{T} \end{pmatrix}\tag{$**$} \]

这里入射光强已经归一化。

非完全偏振光, 实际上是多束完全偏振光作非相干叠加, 即各束光之间无相位关联。因此它在通过偏振片时, 各组分的电矢量独立地被偏振片投影, 所以实验测得的透射光强为各自透过的光强之和, 即

\[I'=\frac{1}{2} \begin{pmatrix} 1,\bf{D} \end{pmatrix}\left[\sum_k^mp_k\begin{pmatrix} 1\\ {\bf{S}}_k^T \end{pmatrix}\right] \]

其中为了对入射总光强归一化, 有$\sum_k^mp_k=1$, $p_k$表示参与构成非完全偏振光的各个完全偏振光的强度比例.

于是得出结论：在讨论非完全偏振光透过偏振片后的光强大小时, Stokes参量是可加的。于是$(**)$式对非完全偏振光依然成立。

因为Stokes参量的可加性, 对于非完全偏振光, $(*)$式可以进一步改写为

\[\begin{pmatrix} S_0\\S_1\\S_2\\S_3 \end{pmatrix}=\sum_k^mp_k \begin{pmatrix} \text{tr}( \hat{\rho}_k\hat{I})\\ \text{tr}( \hat{\rho}_k\hat{\sigma}_z)\\ \text{tr}( \hat{\rho}_k\hat{\sigma}_x)\\ \text{tr}( \hat{\rho}_k\hat{\sigma}_y) \end{pmatrix}=\begin{pmatrix} \text{tr}( \hat{\rho}\hat{I})\\ \text{tr}( \hat{\rho}\hat{\sigma}_z)\\ \text{tr}( \hat{\rho}\hat{\sigma}_x)\\ \text{tr}( \hat{\rho}\hat{\sigma}_y) \end{pmatrix} \tag{$***$} \]

其中$\hat{\rho}=\sum_k^mp_k\hat{\rho}_k$是混合态密度矩阵。于是$(**)$式是普遍的, 对于完全偏振和非完全偏振光都成立, 只不过非完全偏振光的密度矩阵是各个完全偏振光密度矩阵组成的混合态密度矩阵。

偏振度的定义是从实验出发的：一束非完全偏振光入射, 垂直通过一偏振片, 测量通过后的光强, 遍历所有的偏振方向, 得到光强最大值和最小值, 由此定义偏振度偏振度的定义为

\[P=\frac{I_\max-I_\min}{I_\max+I_\min} \]

对于给定Stokes参量$(1,{\bf{S}})^\text{T}$的非完全偏振光, 须求其通过某方向偏振片后的光强, 并遍历偏振方向$(1,{\bf{D}})^\text{T}$, 才能由此算出偏振度。利用$(**)$式, 设${\bf{D}}=(d_1,d_2,d_3)$, 这个问题等价于求函数

\[w=\frac{1}{2}+\frac{1}{2}(d_1S_1+d_2S_2+d_3S_3) \]

在给定诸$S_i$时的最大值和最小值。注意问题的约束为$d_1^2+d_2^2+d_3^2=1$。该问题是线性规划, 可行域为单位球面, 目标函数是一个平面, 法向量为$(S_1,S_2,S_3)$, 根据几何位置关系可得最大值最小值为

\[\begin{aligned} w_\max&=\frac{1}{2}+\frac{1}{2}\sqrt{S_1^2+S_2^2+S_3^2}\\ w_\min&=\frac{1}{2}-\frac{1}{2}\sqrt{S_1^2+S_2^2+S_3^2} \end{aligned} \]

于是由此得出偏振度为$P=\sqrt{S_1^2+S_2^2+S_3^2}$. 这就是一般情况下, 偏振度和归一的Stokes参量的关系。

Poincare球、Bloch球及其与Stokes参量的关系

对于非完全偏振光，但光强归一化的Stokes参量（第一个分量为1），若采用偏振椭圆方位角的形式将其表示为（后三个分量平方之和开方等于常数偏振度$P$，因此不失一般性）

\[S=(1,P\cos2\psi\cos2\chi,P\sin2\psi\cos2\chi,P\sin2\chi)^\text{T} \]

并将后三个分量建立三维坐标，则每一个Stokes参量都对应于单位球面内的一个点（或者更准确地说，对应于一个矢量），且两个方位角有几何意义，如下图所示。这个球就是Poincare球，或者叫做庞加莱球、邦加球。

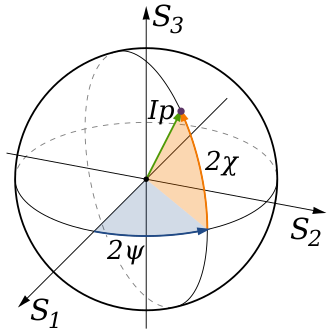
很明显当偏振度$P=1$时，点位于单位球面上。注意到在上面图示中可以引入新变量$\gamma=\pi/2-2\chi$，这样变量$(2\psi,\gamma)$就是一般球坐标中的方位角和极角。

在二能级系统的算符空间内（Hilbert-Schmidt内积空间）任何二能级混合态的密度矩阵都可以写为四个“基矢量”（这里是算符）的叠加（见任意一本量子信息的书）

\[\rho=\frac{I}{2}+\frac{{\vec{r}}\cdot{\vec{\sigma}}}{2} \]

其中叠加系数$\vec{r}$是实的单位矢量，投影可反求出系数${\vec{r}}=\text{tr}(\rho{\bf\sigma})$，根据$(***)$式可得$\vec{r}=(S_1,S_2,S_3)$，它恰好就是即上图中位于单位球面内的那个矢量，注意到$|\vec{r}|=P$。

另一方面，在量子力学中，对于任意一个二能级混合态，都能在Bloch球中表示出来。若设某混合态为$\rho$，则按分解$\rho=\frac{I}{2}+\frac{{\bf{r}}\cdot{\bf{\sigma}}}{2}$得到的矢量$\vec{r}$就是Bloch矢量，且$|\vec{r}|\leqslant1$，当取等号时代表纯态。所以这里的Poincare球和Bloch球完全相同：偏振态也可用一个三维实矢量表示，该矢量模长代表“纯”度或偏振度。只不过在Bloch球中，常用的角度变量不是$\chi$，而是极角$\gamma$.

参考文献
[1]. Rev. Mod. Phys. 33: 8

Jones矢量、Stokes参量、Poincare球、Bloch球

Jones矢量

偏振椭圆

Stokes参量和偏振度

Poincare球、Bloch球及其与Stokes参量的关系

推荐阅读