时间戳

首页 > 技术文章 > 信号与系统04 离散时间傅里叶变换

信号与系统04 离散时间傅里叶变换

wreng 2021-09-26 17:05 原文

1. 离散时间傅里叶变换

1.1. 周期序列的离散傅里叶级数 DFS

连续时间周期信号可以表示成一系列复指数信号的线性加权之和（\(FS\)），离散的周期序列也可以表示成傅里叶级数的形式。

1.1.1. 计算公式

设离散周期序列 \(x[n]\) 的周期为 \(N\)，则基频为 \(\Omega_0 = \frac{2\pi}{N}\)，傅里叶系数对为：

\[\begin{aligned} X[k] &= \frac{1}{N} \sum_{n=<N>} x[n] e^{-j\Omega_0 kn}\\ x[n] &= \sum_{k=<N>} X[k] e^{j\Omega_0 kn} \end{aligned} \]

1.1.2. 离散傅里叶级数的性质

与连续时间周期信号相比，离散周期序列的傅里叶级数有以下区别：

  • 有限性。\(x[n]\) 的傅里叶系数 \(X[k]\) 是有限的，为 \(N\) 项，而连续时间的周期信号傅里叶系数一般是无限的；
  • 周期性。\(X[k]\) 具有周期性，周期为 \(N\)，因此任取一个周期内(\(k\in[k_0, k_0+N-1]\))的傅里叶级数，都可以唯一确定原来的序列。
  • 不存在收敛问题。不同于连续时间傅里叶级数，任何一个离散周期序列均可以通过有限项的傅里叶级数来表示，因此不存在收敛问题，也不存在吉伯斯现象。

产生与连续时间信号傅里叶级数不同的原因是：离散复指数信号的周期性，频率相差 \(2\pi\) 的离散复指数信号是相同，因此对于 \(e^{j\Omega_0 k n}\) 只有 \(N\) 个不同的谐波分量。

\[e^{j\Omega_0 (k+N) n} = e^{j\Omega_0 k n} \]

1.2. 离散时间傅里叶变换 DTFT

1.2.1. 计算公式

\[\begin{aligned} X(e^{j\Omega}) &= \sum_{n=-\infty}^{\infty} x[n] e^{-jn\Omega}\\ x[n] &= \frac{1}{2\pi} \int_{<2\pi>} X(e^{j\Omega}) e^{jn\Omega} d \Omega \end{aligned} \]

其中，\(X(e^{j\Omega})e^{jn\Omega}\) 是周期函数，周期为 \(2\pi\)，所以积分区间可以是任意长度为 \(2\pi\) 的区间。

推导过程：

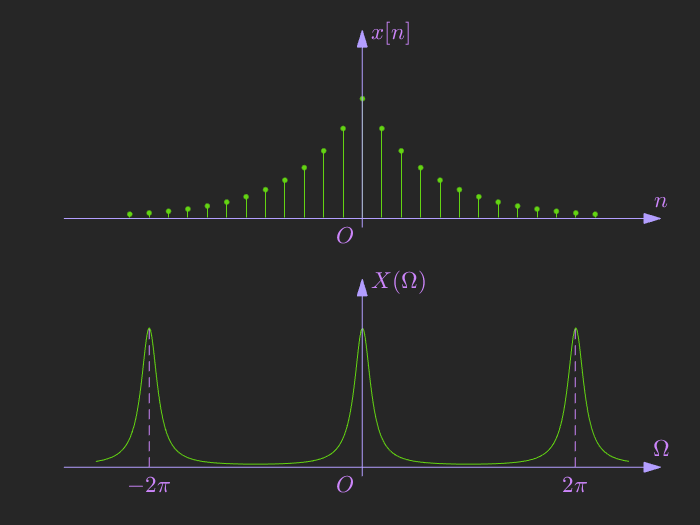
  1. 非周期序列 \(x[n]\) 可以等效为一个周期无限长的周期序列 \(\tilde{x}[n]\)。\(x[n]\) 相当于 \(\tilde{x}[n]\) 的一个周期，当周期 \(N\) 越大的时候，\(\tilde{x}(n)\) 有更大的一部分与 \(x[n]\) 等效，即

\[x[n] = \lim_{N \to +\infty} \tilde{x}[n] \]

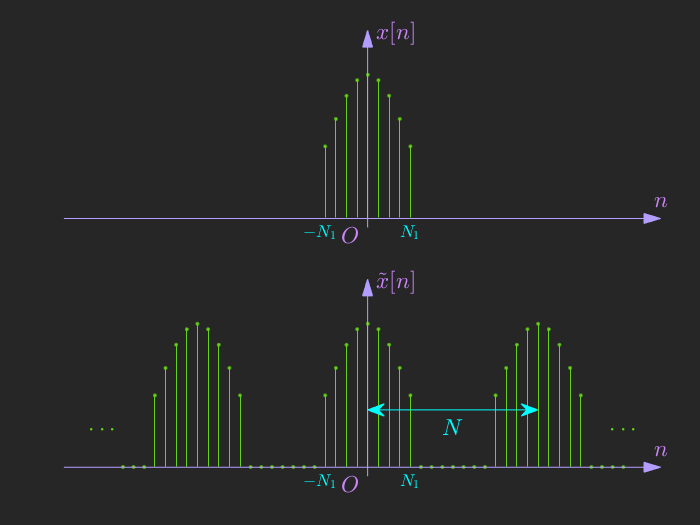
  1. 对周期序列 \(\tilde{x}[n]\) 进行傅里叶级数展开，即

    \[\tilde{X}[k] = \frac{1}{N} \sum_{n=<N>} x[n] e^{-j\frac{2\pi}{N}kn} \]

    考虑到 \(x[n]\) 的非零区间为 \([-N_1,N_1]\)，可以令在此区间的傅里叶级数的包络为

    \[X(e^{j\Omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-jn\Omega} \]

    傅里叶系数与包络的关系为

    \[X[k] = \frac{1}{N} X(e^{j\Omega}) |_{\Omega = k\Omega_0} \]

  2. 周期信号可以表示为包络的等间隔采样，即

    \[ \begin{aligned} \tilde{x}[n] &= \sum_{k=<N>} \frac{1}{N} X(e^{k\Omega_0}) e^{j\Omega_0 kn}\\ &= \frac{1}{2\pi} \sum_{k=<N>} X(e^{k\Omega_0}) e^{j\Omega_0 kn} \Omega_0 \end{aligned} \]

  3. 当周期 \(N \to +\infty\) 时，有\(\tilde{x}[n] \to x[n]\)，\(\Omega_0 \to 0\)，则求和中的每一项表示的物理意义是一个宽度为 \(\Omega_0\)，高度为 \(X(k\Omega_0) e^{j\Omega_0 kn}\) 的矩形的面积。根据微积分的定义，可以将其改写为积分的形式。总共有 \(N\) 个宽度为 \(\Omega_0\) 的矩形，所以最终的积分区间为 \(N \times \Omega_0 = 2\pi\)，

    \[x[n] = \frac{1}{2\pi} \int_{<2\pi>} X(e^{j\Omega}) e^{j\Omega n} d\Omega \]

收敛条件：

  1. 上面的推导虽然是有限长的序列的情况，但对于某些的无限长的序列也是成立的。
  2. 要求序列必须绝对可和或者序列的能量是有限的（有限长的序列都满足，无限长的必须满足此条件）

    \[\sum_{n=-\infty}^{+\infty} |x[n]| < \infty, \quad \sum_{n=-\infty}^{+\infty} |x[n]|^2 < \infty \]

1.2.2. 性质

1.2.2.1. 唯一性

序列与离散时间的傅里叶变换是一一对应的。

1.2.2.2. 奇偶不变性

离散时间傅里叶变换不改变奇偶性，即奇序列的离散时间傅里叶变换仍是奇函数，偶序列的离散时间傅里叶变换仍是偶函数。

1.2.2.3. 周期性

  • \(X(e^{j\Omega})\) 是一个周期函数，周期为 \(2\pi\)，\(X(e^{j\Omega}) = X(e^{\Omega + 2\pi})\)；
  • 靠近 \(\pi\) 的奇数倍为信号的高频部分；
  • 靠近 \(\pi\) 的偶数倍为信号的低频部分。

1.2.2.4. 线性

\[ax_1[n] + bx_2[n] \leftrightarrow aX_1(e^{j\Omega}) + bX_2(e^{j\Omega}) \]

1.2.2.5. 共轭对称性

\[x^*[n] \leftrightarrow X^*(e^{-j\Omega}) \]

  • 信号的偶分量 \(x_e[n]\) 对应 \(\mathrm{Re}[X(e^{j\Omega})]\)；
  • 信号的奇分量 \(x_o[n]\) 对应 \(\mathrm{Im}[X(e^{j\Omega})]\)；
  • 如果 \(x[n]\) 为实信号，则 \(X(e^{j\Omega})\) 是共轭对称函数（实部为偶，虚部为奇/幅度为偶，相位为奇），实部就相当于 \(X(e^{j\Omega})\) 的偶分量，虚部就相当于 \(X(e^{j\Omega})\) 的奇分量。（特别注意，前提条件是实序列）
  • 根据奇偶不变性，若 \(x[n]\) 为实偶序列，则 \(X(e^{\Omega})\) 只存在为偶分量的实部；若 \(x[n]\) 为实奇序列，则 \(X(e^{\Omega})\) 只存在为奇分量的虚部；

1.2.2.6. 时移、频移特性

  • 时移特性

    \[x[n - n_0] \leftrightarrow X(e^{j\Omega}) e^{-j\Omega n_0} \]

  • 频移特性

    \[x[n] e^{j\Omega_0 n} \leftrightarrow X(e^{j(\Omega - \Omega_0)}) \]

1.2.2.7. 尺度变换特性

离散序列的时间尺度的变换定义为：（要求 \(k\) 是一个正整数）

\[x_{(k)}[n] = \begin{cases} x[n/k]&, n 是 k 的倍数\\ 0 &, 其他 \end{cases} \]

例如：\(k=3\)，相当于在原序列的每项之间插\((3-1)\)个0，则在频域上傅里叶变换被压缩了，

\[x_{(k)}[n] \leftrightarrow X(e^{jk\Omega}), \quad k\ge1 \]

【例】
已知序列 \(x[n] = \delta[n+1] + \delta[n-1]\)，可以分别求得:

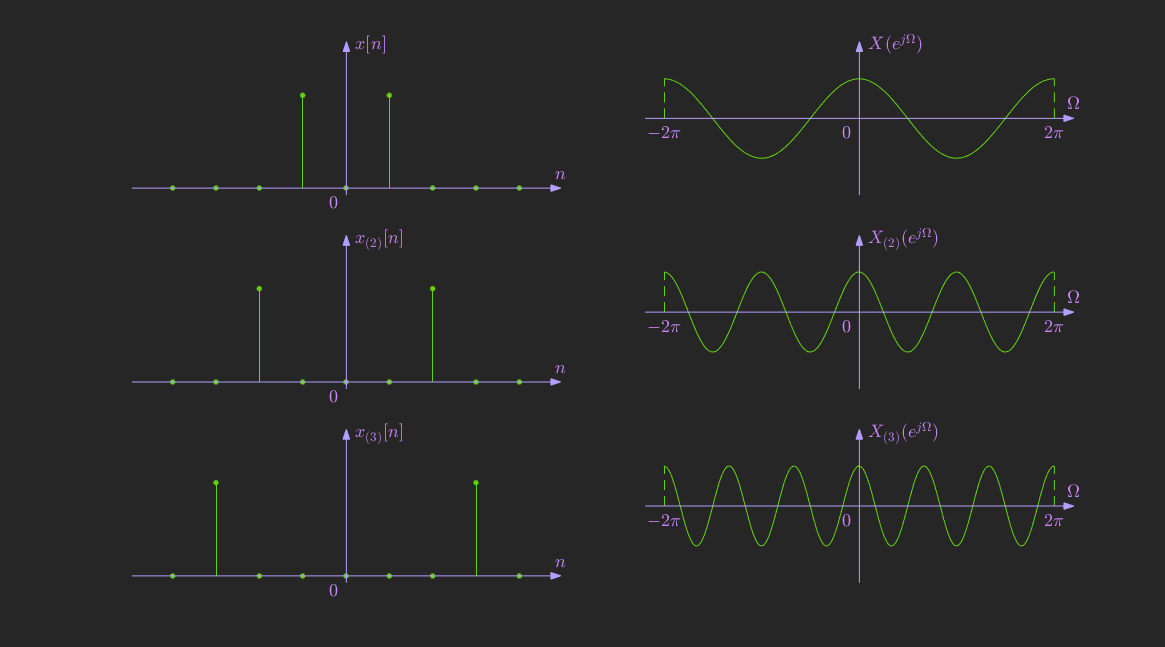
\[\begin{aligned} x[n] &\leftrightarrow 2\cos \Omega\\ x_{(2)}[n] &\leftrightarrow 2\cos (2\Omega)\\ x_{(3)}[n] &\leftrightarrow 2\cos (3\Omega)\\ \end{aligned} \]

【注意】

  • 时域扩展后，频域是被压缩了，但是幅度是没发生变换，因为插 0 不会丢失原信号的信息，不会改变序列的总能量；
  • \(k\) 必须是正整数，上式才成立。若 \(k < 1\) 例如 \(k = 1/2\)，相当于从原序列中每隔一个元素抽取一个元素组成一个新的序列，与原序列相比是丢失很多信息的，例如：计算 \(X_k(e^{j\Omega})\) 的过程就是一个累加的过程，显然，抽取之后参与累加的元素变少了，抽取后的傅里叶函数至少在幅度上会发生变化，故上式是不成立的。

1.2.2.8. 差分、求和特性

后向差分特性

\[\triangledown x[n] = x[n] - x[n-1] \leftrightarrow (1-e^{-j\Omega}) X(e^{j\Omega}) \]

求和特性

\[\sum_{k=-\infty}^{n} x[k] \leftrightarrow \frac{1}{1-e^{-j\Omega}} X(e^{jw}) + \pi X(0) \sum_{k=-\infty}^{+\infty} \delta(\Omega - 2\pi k) \]

其中，\(X(0)\) 是 \(x[n]\) 的直流分量，即 \(X(0) = \sum_{k} x[k]\).

1.2.2.9. 频域微分特性

\[(-n) x[n] \leftrightarrow \frac{d X(e^{j\Omega})}{d (j\Omega)}\\ n x[n] \leftrightarrow j\frac{d X(e^{j\Omega})}{dw} \]

频域的微分运算可以转化为时域的乘法运算，因子为 \(-n\).

1.2.2.10. 卷积特性

  • 时域卷积特性

\[x[n] * y[n] \leftrightarrow X(e^{j\Omega}) Y(e^{j\Omega}) \]

  • 频域卷积特性

    \[x[n] y[n] \leftrightarrow \frac{1}{2\pi} X(e^{j\Omega}) \circledast Y(e^{j\Omega}) = \frac{1}{2\pi} \int_{<2\pi>} X(e^{j\eta}) Y(e^{j\Omega-j\eta}) d \eta \]

    其中, \(\circledast\) 表示周期卷积。

    频域卷积有两个重要的应用：

    • 调制，对信号的频谱进行搬移；
    • 加窗，对时域信号进行截断，滤波等。

1.2.2.11. 巴什瓦定律

\[\sum_{n=-\infty}^{+\infty} |x[n]|^2 = \frac{1}{2\pi} \int_{<2\pi>} |X(e^{j\Omega})|^2 d\Omega \]

1.3. 周期序列的离散时间傅里叶变换

周期序列的离散时间傅里叶变换有两种推导方式：

  • 傅里叶级数展开
  • 时域卷积

再推导之前，给出以下离散时间傅里叶变换对：

\[\begin{aligned} e^{j\Omega_0 n} &\leftrightarrow 2\pi \sum_{k=-\infty}^{\infty} \delta(\Omega - \Omega_0 - 2\pi k)\\ \sum_{k=-\infty}^{\infty} \delta[n-kN] &\leftrightarrow \Omega_0 \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_0) \end{aligned} \]

利用傅里叶级数的推导过程

周期序列可以用傅里叶技术表示，即

\[\begin{aligned} \tilde{x}[n] &= \sum_{k=<N>} X[k] e^{j\frac{2\pi}{N}kn}\\ &\leftrightarrow \sum_{k=<N>} 2\pi X[k] \sum_{m=-\infty}^{\infty} \delta(\Omega - \frac{2\pi}{N}k - 2\pi m)\\ &= 2\pi X[0] \sum_{m=-\infty}^{\infty} \delta(\Omega - 2\pi m) \\ &\quad + 2\pi X[1] \sum_{m=-\infty}^{\infty} \delta(\Omega - \frac{2\pi}{N} - 2\pi m)\\ &\quad + 2\pi X[2] \sum_{m=-\infty}^{\infty} \delta(\Omega - \frac{2\pi}{N}\cdot 2 - 2\pi m)\\ &\quad \cdots\\ &\quad + 2\pi X[N-1] \sum_{m=-\infty}^{\infty} \delta(\Omega - \frac{2\pi}{N}\cdot (N-1) - 2\pi m)\\ &= \sum_{k=-\infty}^{+\infty} 2\pi X[k] \delta(\Omega - \frac{2\pi}{N}k) \end{aligned} \]

利用时域卷积性质的推导过程

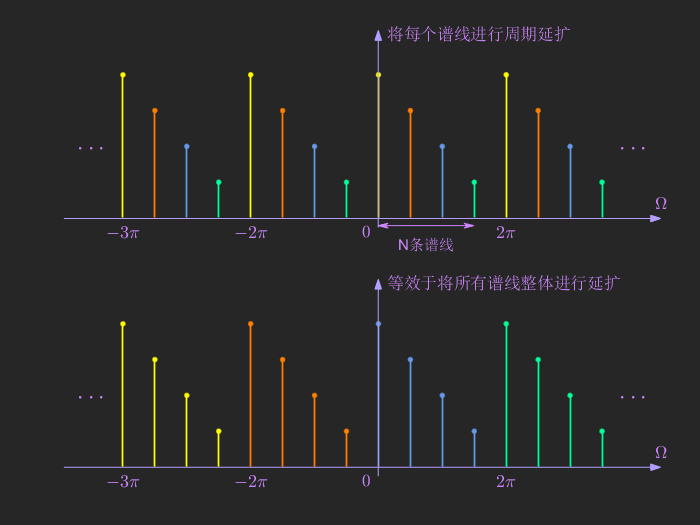
同连续时间信号类似，周期序列 \(\tilde{x}[n]\) 可由非周期序列 \(x[n]\) 进行周期延拓得到，即

\[\tilde{x}[n] = x[n] * \sum_{k=-\infty}^{+\infty} \delta[n-kN] \]

根据时域卷积特性，有

\[\tilde{X}(e^{j\Omega}) \leftrightarrow X(e^{j\Omega}) \cdot \Omega_0 \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_0) = \sum_{k=-\infty}^{+\infty} \Omega_0 X(e^{j\Omega_0}) \delta(\Omega - k\Omega_0) \]

傅里叶级数与离散时间傅里叶变换的关系为：\(X[k] = \frac{1}{N}X(e^{j\frac{2\pi}{N}k})\)，两种推导的方式的最终结果是一致的。

对于周期序列，其离散时间傅里叶变换为一系列的冲激函数，也是一个周期函数。在一个周期内，每个冲激的幅度为该谐波分量傅里叶级数的 \(2\pi\) 倍。

1.4. 常见的离散时间傅里叶变换对

离散时间傅里叶变换的计算实际上就是计算等比数列的求和问题。

在实际中，离散时间傅里叶变换用得比较少，\(z\) 变换比较多些。

下面给出在求系统响应时常见的变换对：

1.4.1. 单边指数序列

\[a^{n} u[n] \leftrightarrow \frac{1}{1-ae^{-j\Omega}},\quad |a|<1 \]

1.4.2. 单位采样序列

\[\delta[n] \leftrightarrow 1\\ \delta[n-n_0] \leftrightarrow e^{-j\Omega n_0} \]

1.4.3. 直流信号

\[1 \leftrightarrow 2\pi \sum_{k=-\infty}^{\infty} \delta(\Omega - 2\pi k)\\ e^{j\Omega_0 n} \leftrightarrow 2\pi \sum_{k=-\infty}^{\infty} \delta(\Omega - \Omega_0 - 2\pi k) \]

1.4.4. 周期样本序列

\[\sum_{k=-\infty}^{\infty} \delta[n-kN] \leftrightarrow \Omega_0 \sum_{k=-\infty}^{\infty} \delta(\Omega - k\Omega_0) \]

直流信号和周期样本序列不能或难以根据定义式求出，其推导过程利用了连续时间采样的一些知识。

1.5. 小结

  • 时域的离散性对应了频域的周期性（非周期离散序列的离散时间傅里叶变换为周期连续函数）
  • 时域的周期性对应了频域的离散性（周期离散序列的离散时间傅里叶变换为周期的离散冲激族）
  • 与连续时间傅里叶变换相比的相同点：唯一性，线性，奇偶不变性，共轭特性，时移频移特性，频域微分特性，时域卷积
  • 与连续时间傅里叶变换相比的不相同点：
    • 周期性：离散时间傅里叶变换为周期函数
    • 时域展缩：序列时域上只能“展”（插0），不能“缩”（抽样）。对于连续时间为 \(f(at)\leftrightarrow \frac{1}{|a|} f(\frac{t}{a})\)，而离散时间为 \(x_{(a)}[n] \leftrightarrow X(e^{ja\Omega})\)
    • 频域卷积特性：离散时间序列对应的是周期卷积
    • 巴什瓦定律：频域的能量的积分区间长度为 \(2\pi\)

推荐阅读