不保证正确. 不保证正确. 不保证正确. 纯属娱乐.
书是亚里夫(Yariv)量子电子学第二版.
6.1
递推公式为\(r_{s+2}-2 b r_{s}+r_{s}=0\), 其中\(b=1-2 \frac{d}{f}+\frac{d^{2}}{2 f^{2}}\), 差分方程的特征方程为
\[x^{2}-2 b x+1=0 \Rightarrow x_{1, {2}} =\frac{1}{2}\left(2 b \pm \sqrt{4 b^{2}-4}\right)=b \pm \sqrt{b^{2}-1}
\]
当\(x\)是实数时\((|b|>1)\), 通解为
\[r_{s}=A x_{1}^{s}+B x_{2}^{s}
\]
不稳定. 当\(x\)不是实数时\((|b|<1)\), 通解为
\[r_{s}=|x|^{s}[A \cos \beta s+B \sin \beta s], \beta : x_{1,2}=|x| e^{ \pm i \beta}
\]
由于\(|x|=1\), 于是有
\[ r_{s}=A \cos \beta s+B \sin \beta s
\]
为稳定振荡.
因此\(|b|<1\), 可以改写为
\[r_{s}=r_{\max } \sin (\beta s+\delta)
\]
又因为\(x_{1,2}=|x| e^{ \pm i \beta}\), 所以\(\cos \beta=b\).
6.2
直接求\(\left[\begin{array}{ll}{A} & {B} \\ {C} & {D}\end{array}\right]\)本征值, \(\lambda=\frac{1}{2}(A+D) \pm \frac{1}{2} \sqrt{A^{2}+D^{2}-2 A D+4 B C}\), 利用\(AD-BC=1\), 得\(\lambda=b \pm i \sqrt{1-b^{2}}\), 其中\(b=\frac{1}{2}(A+D)\).
6.3
薄透镜左侧为平面波, 左界面上各处相位相等, 右侧为球面波, 中心在距离右侧为\(f\)处. 球面波为
\[\frac{A}{r} e^{i k r}, r=\sqrt{x^{2}+y^{2}+z^{2}}
\]
在右侧面上的相位为\(e^{i k \sqrt{x^{2}+y^{2}}+f^{2}}\), 在\(x^2+y^2\ll f^2\)时展开有
\[e^{i k f\left(1+\frac{x^{2}+y^{2}}{2 f^{2}}\right)}=e^{i k f} e^{i k \frac{x^{2}+y^{2}}{f}}
\]
其中\(e^{i k f}\)为全局相位可以丢弃, 于是有效相移为\(e^{i k \frac{x^{2}+y^{2}}{f}}\).
6.4
在\(k=l\)的出射界质界面上有
\[\left\{
\begin{aligned}
r&=\cos \left(\sqrt{\frac{k_{2}}{k}} l\right) r_0\\
r^{\prime}&=-\frac{\sqrt{k_{2}}}{k} \sin \left(\frac{k_{2}}{k} l\right) r_{0}
\end{aligned}
\right.
\]
因为是平行光入射, \(r'_0=0\), 所以上式直接相除得到
\[h=\frac{1}{n_{0}} \sqrt{\frac{k}{k_{2}}} \cot \left(\frac{\sqrt{k_{2}}}{k} l\right)
\]
6.5
因为是轴上点, \(r_0=0\), 于是
\[\Big|\frac{r}{r^{\prime}} \Big|=\sqrt{\frac{k}{k_{2}}} \tan \left(\frac{k_{2}}{k} b\right)
\]
就是像距.
6.7
设透镜\(f\)在入射光束束腰后\(d\)位置, 则传输矩阵为
\[\left[\begin{array}{cc}{A} & {B} \\ {C} & {D}\end{array}\right]=\left[\begin{array}{cc}{1} & {0} \\ {-\frac{1}{f}} & {1}\end{array}\right]\left[\begin{array}{ll}{1} & {d} \\ {0} & {1}\end{array}\right]=\left[\begin{array}{cc}{1} & {d} \\ {-\frac{1}{f}} & {1-\frac{d}{f}}\end{array}\right]
\]
\[q_{2}=\frac{f q_{1}+f d}{-q_{1}+f-d}
\]
而\(q_3=q_2+l\), 令\(\operatorname{Re}\left(\frac{1}{q_{3}}\right)=0\), 得到
\[l=\frac{z_{0}^{2} f+(d-f) f d}{z_{0}^{2}+(d-f)^{2}}=f+\frac{f^{2}(d-f)}{(d-f)^{2}+z_{0}^{2}}
\]
其中\(z_{0}=\frac{\pi w_{0}^{2} n}{\lambda}\). 利用
\[\frac{\text{Im}\left(\frac{1}{q_{1}}\right)}{\text{Im}\left(\frac{1}{q_{3}}\right)}=\left(\frac{\omega_{3}}{\omega_{0}}\right)^{3} \Rightarrow w_{3}^{3}=w_{0}^{3} \frac{-(l-f)^{3}}{(f-d)(f-l)+f d+(f-d) l}
\]
6.8
传输矩阵为
\[\left[\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right]\left[\begin{array}{cc}{1} & {0} \\ {0} & {n}\end{array}\right]\left[\begin{array}{cc}{1} & {l_{2}-l_{1}} \\ {0} & {1}\end{array}\right]\left[\begin{array}{ll}{1} & {0} \\ {0} & {\frac{1}{n}}\end{array}\right]\left[\begin{array}{ll}{1} & {l_1} \\ {0} & {1}\end{array}\right]=
\left[\begin{array}{ll}{1} & {l_{1}+l+\frac{l_{2}-l_{1}}{n}} \\ {0} & {1}\end{array}\right]
\]
所以相当于自由传播有
\[q=q_{0}+l_{1}+l+\frac{l_{2}-l_{1}}{n}
\]
所以
\[\theta \simeq \frac{\lambda}{\pi w_{0} n}
\]
6.9
传输矩阵为
\[\left[\begin{array}{ll}{1} & {L} \\ {0} & {1}\end{array}\right]\left[\begin{array}{cc}{1} & {0} \\ {-\frac{1}{f}} & {1}\end{array}\right]\left[\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right]=\left[\begin{array}{cc}{1-\frac{L}{f}} & {l+L-\frac{l L}{f}} \\ {-\frac{1}{f}} & {-\frac{l}{f}+1}\end{array}\right]
\]
所以
\[q=\frac{q_{0}(f-L)+f(l+L)-lL}{-q_{0}+f-l}
\]
令\(\operatorname{Re}\left(\frac{1}{q_{}}\right)=0\),
\[\frac{1}{q}=\frac{\left(f-l-i z_{0}\right)\left[f(l+L)-l L-i z_{0}(f-L)\right]}{[f(L+l)-L l]^{2}+z_{0}^{2}(f-L)^{2}}
\]
因此得到关于\(f\)的二次方程
\[(l+L) f^{2}-\left(l^{2}+z_{0}^{2}+2 l L\right) f+L\left(l^{2}+z_{0}^{2}\right)=0
\]
因为除了\(f\)以外各个参数已定, 因此两个解只有光斑尺寸不同.
6.11
考虑波包
\[A(z, t)=\int_{-\infty}^{\infty} G(\Delta \omega) e^{i[\Delta \omega t-\Delta k(\omega) z]} d(\Delta\omega)
\]
作二阶展开
\[\Delta k(\omega)=\left.\frac{d k}{d \omega}\right|_{\omega=\omega_{0}} \cdot \Delta \omega+\frac{1}{2}\left.\frac{d^{2} k}{d \omega^{2}}\right|_{\omega=\omega_{0}} \cdot(\Delta \omega)^{2}
\]
令\(a=\frac{1}{2} \frac{d^{2} k}{d \omega^{2}} \Big|_{\omega=\omega_0}\)则有
\[A(z, t)=\int_{-\infty}^{\infty} G(\Delta \omega) e^{i\left[\Delta \omega t-\frac{z}{v_{g}} \Delta \omega+a(\Delta \omega)^{2} z\right]}
\]
取高斯波包\(G(\Delta \omega)=\sqrt{\frac{\pi}{2}} e^{-\Delta \omega^{2} / 4 \alpha}\), 其中脉冲宽度\(\tau_{0}=\sqrt{\frac{2 \ln 2}{\alpha}}\), 带入积分计算得到
\[A(z, t)=N \exp [i \varphi(z, t)] \exp \left(\frac{\left(t-\frac{z}{v g}\right)^{2}}{\frac{1}{\alpha}+16 \alpha a^{2} z^{2}}\right)
\]
其中\(N\)为归一化因子, 而\(\varphi(z,t)\)是一实函数, 由此得脉冲宽度
\[\tau(z)=\sqrt{\frac{2 \ln 2}{\alpha}} \sqrt{1+16 a^{2} \alpha^{2} z^{2}}\simeq \tau_{0} 4 |a|\alpha z=4 \ln 2 \frac{L}{\tau_{0}} \frac{d^{2} k}{d w^{2}}\bigg|_{w=w_{0}}
\]
最后的\(z\)取\(L\), 而且
\[\frac{d^{2} k}{d \omega^{2}}\bigg|_{\omega=\omega_{0}}= \frac{d}{d \omega} \frac{d k}{d \omega}=-\frac{1}{v_{g}^{2}} \frac{d v_{g}}{d \omega}
\]
或者, 频率为\(\omega_{0}+\frac{1}{2} \Delta \omega\)的部分和\(\omega_{0}-\frac{1}{2} \Delta \omega\)的部分, 在不同时刻到达\(L\)处, 时间差为
\[\Delta\tau=\frac{L}{v_{g}\left(\omega+\frac{1}{2} \Delta w\right)}-\frac{L}{v_{g}\left(\omega-\frac{1}{2} \Delta \omega\right)}=\left(\frac{1}{v_g+\frac{d v_{g}}{d \omega} \big| _{\omega=\omega_{0}} \cdot \frac{1}{2} \Delta \omega}-\frac{1}{v_g-\frac{d v_{g}}{d \omega} \big| _{\omega=\omega_{0}} \cdot \frac{1}{2} \Delta \omega}\right)\\=-\frac{L}{\nu_{g}^{2}}\left.\frac{d v_{g}}{d \omega}\right|_{\omega=\omega_{0}} \cdot \Delta \omega
\]
其中\(\Delta \omega=\frac{1}{\pi \tau_{0}}\), 于是得到题中给出的展宽.
6.12
光斑尺寸由下式决定,
\[\omega=\sqrt{\frac{\lambda}{\pi}}\left(\frac{1}{n n_{2}}\right)^{\frac{1}{4}}
\]
而展宽后的总脉冲宽度为
\[\tau+\Delta \tau=\frac{L}{v_{g}^{2}} \frac{n_{2} / n}{k^{3}}(l+m+1)^{2} \frac{1}{\pi \tau}+\tau
\]
从而每秒最多发送的脉冲数量, 由上面的脉冲宽度决定, 即\(1/(\tau+\Delta\tau)\).
6.13
令\(\psi(x, y)=f(x) g(y)\), 则分离变量可得
\[\left\{\begin{array}{l}{\frac{f^{\prime \prime}(x)}{f(x)}-k^{2} \frac{n_{2}}{n} x^{2}=-\lambda_x} \\ {\frac{g^{\prime \prime}(y)}{g(y)}-k^{2} \frac{n_{2}}{n} y^{2}=-\lambda_{y}} \\ {k^{2}-\beta^{2}-\lambda_{x}-\lambda_{y}=0}\end{array}\right.
\]
再引入下面变量进行无量纲化处理
\[\xi=\frac{\sqrt{2} x}{\omega}, \omega=\sqrt{\frac{\lambda}{\pi}}\left(\frac{1}{n \pi_{2}}\right)^{\frac{1}{4}}
\]
得到\(f^{\prime \prime}(\xi)+\left(\lambda^{\prime}-\xi^{2}\right) f(\xi)=0\), 所以\(\lambda^{\prime}=2 l+1\), 而
\[f(x)=H\left(\frac{\sqrt{2} x}{\omega}\right) e^{-\left(\frac{x}{\omega}\right)^{2}}
\]
对\(y\)也类似处理, 有
\[\psi(x, y)=E_{(l, m)} H_{l}\left(\sqrt{2} \frac{x}{\omega}\right) H_{m}\left(\sqrt{2} \frac{y}{\omega}\right) e^{-\frac{x^{2}+y^{2}}{\omega^{2}}}
\]
再利用\(k^{2}-\beta^{2}-\lambda_{x}-\lambda_{y}=0\)可得
\[\beta_{l, m}=k \sqrt{1-\frac{2}{k} \sqrt{\frac{n_{2}}{n}}(l+m+1)}
\]
7.1
利用\(Q=\omega t_{c}\), \(t_{c}=\frac{n l}{c\left[\alpha l+\left(1-\sqrt{R_{1} R_{2}}\right)\right]}\)对光学腔和微波腔几乎相同, 所以差异仅仅在\(\omega\)上. 因此光学腔的\(Q\)值比微波腔高\(3\)到\(6\)个数量级.
7.2
作图如下
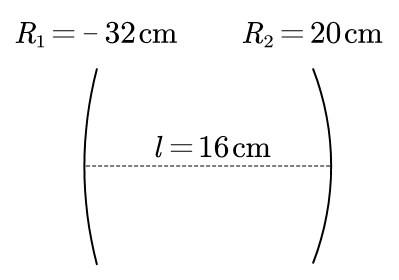
解方程
\[z_1+z_0/z_1=-32\\
z_2+z_0/z_2=20\\
z_2-z_1=16
\]
可得\(z1=-3.2,z_2=12.8,z_0=9.6\), 单位厘米. 根据\(1/q_0=-i\lambda/(\pi\omega_0^2 n)=-iz_0\)可得束腰尺寸\(\omega_0=0.175\text{mm}\). 根据高斯光束的传播规律\(q_{1,2}=q_0+l\)可得\(\omega_1=0.184\text{mm}\), \(\omega_2=0.291\text{mm}\).
7.3
反射镜的不完全反射引起的损耗为\(0.5%\), 因此\((1-0.5 \%) \cdot(1-x) \leqslant 97 \% \Rightarrow x \geqslant 2.51 \%\), 由图估计出\(\frac{a^{2} n}{\lambda l} \leq 1.0\), 因此\(a \leqslant\). 取\(\frac{a^{2} n}{\lambda l}=1.0\), 则基模衍射损耗约为\(10^{-4}\), 因此总损耗\(1-\left(1-10^{-4}\right) \times 0.995 \approx 0.51 \%\).
7.4
令\(\frac{l}{R}=x, \frac{l}{R_{2}}=y\), 则稳定条件的方程约束写为\(0 \leq(1-x)(1-y) \leq 1\), 注意\(\frac{1}{x}+\frac{1}{y}=1\)和\((x-1)(y-1)=1\)是同一条曲线. 边界\((x-1)(y-1)=1\)把平面分为6块, 对每一块要么全部满足约束要么全部违反约束.
7.5
透镜阵列的每个周期的传输矩阵为
\[\left(\begin{array}{rr}{1} & {0} \\ {-\frac{2}{R_{1}}} & {1}\end{array}\right)\left(\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {\frac{2}{R_{2}}} & {1}\end{array}\right)\left(\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right)=\left(\begin{array}{ll}{A} & {B} \\ {C} & {D}\end{array}\right)
\]
当\(r_{n+1}=A r_{n}+B r_{n}^{\prime}<r_{n}\)时有汇聚作用. 计算得出其中,
\[\begin{array}{l}{A=1+\frac{2 l}{R_{2}}} \\ {B=l\left(2+\frac{2 l}{R_{2}}\right)}\end{array}
\]
7.6
由于是对称腔型, 束腰位于腔中心于是, \(q_{1}=q_{0}+\frac{l}{2}\), 而\(q_1\)对应的\(R\)就是腔镜的\(R\), 即
\[\operatorname{Re}\left[\frac{1}{q_{1}}\right]=\frac{1}{R} \Rightarrow Z_{0}=\sqrt{\frac{1}{2} R l-\frac{1}{4} l^{2}}
\]
因此
\[\omega_{0}^{2}=\frac{\lambda}{\pi n} \sqrt{\frac{1}{2} R l-\frac{1}{4} l^{2}}\\
\omega(e)=\omega_{0} \sqrt{1+\left(\frac{ l}{2 z_{0}}\right)^{2}}
\]
7.7
由
\[\left\{\begin{array}{l}{R_{1}=-\left(z_{1}+\frac{z_{0}^{2}}{z_{1}}\right)} \\ {R_{2}=z_{2}+\frac{z_{0}^{2}}{z_{2}}}\end{array}\right.
\]
代入\(\left(1-\frac{l}{R_{1}}\right)\left(1-\frac{l}{R_{2}}\right)\)得
\[g_{1} g_{2}=\frac{\left(z_{0}^{2}+z_{1} z_{2}\right)^{2}}{\left(z_{1}^{2}+z_{0}^{2}\right)\left(z_{2}^{2}+z_{0}^{2}\right)} \geqslant 0
\]
再设\(g_{1} g_{2} \leqslant 1\), 并展开消项, 得到\(2 z_{1} z_{2} \leqslant z_{1}^{2}+z_{2}^{2}\), 所以确实有\(g_{1} g_{2} \leqslant 1\).
7.8
传输矩阵为
\[\left(\begin{array}{cc}{1} & {0} \\ {-\frac{2}{R}} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {\frac{l}{2}} \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {-\frac{1}{f}} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {\frac{l}{2}} \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {-\frac{2}{R}} & {1}\end{array}\right)\left(\begin{array}{ll}{1} & {\frac{l}{2} } \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {-\frac{1}{f}} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {\frac{l}{2} } \\ {0} & {1}\end{array}\right)=\left(\begin{array}{ll}{A} & {B} \\ {C} & {D}\end{array}\right)
\]
稳定条件为
\[\left|\frac{A+D}{2}\right| \leqslant 1
\]
于是得到稳定条件为
\[\Bigg|\frac{l^{2}(l-2 R)^{2}+8 f^{2}\left(2 l-4 l R+R^{2}\right)-8 f l\left(l^{2}-3 l R+2 R^{2}\right)}{8 f^{2} R^{2}}\Bigg|\leqslant1
\]
7.9
以第二面反射镜处为参考面, 则传输矩阵为
\[\left(\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {-\frac{2}{R_{1}}} & {1}\end{array}\right)\left(\begin{array}{ll}{1} & {l} \\ {0} & {1}\end{array}\right)\left(\begin{array}{cc}{1} & {0} \\ {-\frac{2}{R_{2}}} & {1}\end{array}\right)=\left(\begin{array}{ll}{\frac{4 l^{2}+R_{1} R_{2}-2 l\left(2 R_{1}+R_{2}\right)}{R_{1} R_{2}}} & {l\left(2-\frac{2 l}{R l}\right)} \\ {-2 \frac{\left(-2 l+R_{1}+R_{2}\right)}{R_{1} R_{2}}} & {l-\frac{2 l}{R l}}\end{array}\right)
\]
由7.2-7式可得\(R(2镜)=\frac{2B}{D-A}\)将矩阵元带入化简得\(\frac{2B}{D-A}=R_2\). 对于\(R_1\)镜面, 选取参考面在\(R_1\)处, 也可以得到类似证明.
7.10
由7.2-3可得
\[\frac{1}{q}=\frac{C q+D}{A q+B}=\frac{C+D /q}{A+B/q}
\]
设函数
\[f(x)=\frac{C+D x}{A+B x}, \delta f(x)=f(x+\Delta x)-f(x) \simeq \frac{\Delta x}{(A+B x)^{2}}
\]
在上式右边的\(x\)中带入稳态解7.2-5得
\[\delta f=\frac{1}{\left[\frac{A+D}{2} \pm i \sqrt{1-\left(\frac{A+D}{2}\right)^{2}}\right]^{2}} \cdot \Delta x
\]
上式分母的方括号中的复数, 它的模为\(1\), 可写为\(e^{ \pm i \theta}\), 其中\(\theta\)满足\(\cos \theta=\frac{1}{2}(A+D)\), 所以\(\delta f=e^{\mp i2 \theta} \cdot \Delta x\), 其中\(\Delta x\)代表\(\Delta(1/q)\), 而\(\delta f\)代表\(\delta(1/q)\). 显然当满足稳定条件的时候, 即\(\theta\)是实数, 则有
\[\left|\delta\left(\frac{1}{q}\right)\right|=\left|\Delta\left(\frac{1}{q}\right)\right|
\]
8.1
式8.3-4显然满足\(W_{感应}/W_{自发}=n\). 式8.5-11给出,
\[W_{感应}/W_{自发}=\frac{W_{21}}{A}=\frac{c^{3}}{8 \pi n^{3} h\nu} \rho(\nu)
\]
带入8.5-4可得
\[\frac{W_{21}}{A}=\frac{1}{e^{h \nu / k T}-1}
\]
是\(\nu\)模式上的平均光子占据数, 即光子数.
8.2
以8.7-4式在\(I_\nu=0\)时计算.
\[\gamma(\nu)=\frac{\Delta N_{0} \lambda^{2} g(\nu)}{8 \pi n^{2} t}
\]
其中的\(g(\nu)\)取8.6-10的峰值\(\frac{2 \sqrt{\ln 2}}{\sqrt{\pi} \Delta \nu_{D}}\), 而\(\Delta \nu_{D}\)由下面条件估计,
\[\Delta \nu_{D}=c \cdot \Delta\left(\frac{1}{\lambda}\right)
\]
其中\(\Delta(1/\lambda)=400\text{cm}^{-1}\), 由此直接可计算出\(\gamma(\nu_0)\).
8.3
按照\(r=r_0\cos(\omega t)\)简谐振动的电子, 能量为
\[E=\frac{1}{2} m \dot{r}^{2}+\frac{1}{2} m \omega^{2} r^{2}=\frac{1}{2} m \omega^{2} r_{0}^{2}
\]
按照拉莫尔公式, 辐射功率为
\[P=\frac{e^{2} \dot{r}^{2}}{6 \pi \varepsilon_{0} c^{3}}
\]
于是寿命为
\[t_{寿命}=\frac{E}{P}=\frac{6 \pi \varepsilon_{0} c^{3} m}{e^{2} \omega^{2}}=\frac{3 \varepsilon_{0} c^{3} m}{2 \pi e^{2} \nu^{2}}
\]
8.5
令\(\dot{\sigma}_{21}=0, \dot{\rho}_{11}-\dot{\rho}_{22}=0\)得到
\[i\left(\omega-\omega_{0}\right) \sigma_{21}+i \Omega\left(\rho_{11}-\rho_{22}\right)-\frac{\sigma_{21}}{T_{2}}=0\\
i 2 \Omega\left(\sigma_{21}-\sigma_{21}^{*}\right)-\frac{\rho_{11}-\rho_{22}-\left(\rho_{11}-\rho_{22}\right)_{0}}{\tau}=0
\]
得到
\[\sigma_{21}=\frac{i \Omega\left(\rho_{11}-\rho_{22}\right)}{\frac{1}{T_{2}}-i\left(\omega-\omega_{0}\right)}
\]
代回并得到
\[\rho_{11}-\rho_{22}=\left(\rho_{11}-\rho_{22}\right)_0 \frac{1+\left(\omega-\omega_{0}\right)^{2} T_{2}^2}{4 \Omega^{2} T_{2} \tau+1+\left(\omega-\omega_{0}\right)^{2} T_{2}^{2}}
\]
再次代回得到
\[\text{Im}\left[\sigma_{21}\right]=\frac{\Omega T_{2}\left(\rho_{11}-\rho_{22}\right)_0}{1+\left(\omega-\omega_{0}\right)^{2} T_{2}^{2}+4 \Omega^{2} T_{2} \tau}\\
\text{Re}\left[\sigma_{21}\right]=\frac{-\left(\omega-\omega_{0}\right) \Omega T_{2}^{2}\left(\rho_{11}-\rho_{22}\right)_{0}}{1+\left(\omega-\omega_{0}\right)^{2} T_{2}^{2}+4 \Omega^{2} T_{2} \tau}
\]
8.6
\[\chi(\omega)=\chi^{\prime}(\omega)-i \chi^{\prime \prime}(\omega)\\=\frac{\mu \Delta N_{0}}{\varepsilon_{0} \hbar}\frac{\omega-\left[\omega_{0}-\left(i / T_{2}\right)\right)}{\left\{\omega-\left[\omega_{0}-\left(i / T_{2}\right) \sqrt{\left(1+s^{2}\right)}\right]\right\}\left\{\omega-\left[\omega_{0}+\left(i / T_{2}\right) \sqrt{1+s^{2}}\right]\right\}}
\]
在\(s^{2}=\mu^{2} E_0^{2} T_{2} \tau / \hbar^{2} \propto E_{0}^{4}=0\)时,
\[\chi(\omega)=-\frac{\mu \Delta N_{0}}{\varepsilon_{0} \hbar} \frac{1}{\omega-\left[\omega_{0}+\left(i / T_{2}\right)\right]}
\]
在\(\omega\)下半平面有单极点, 满足Kramers-Kronig定理的条件.
9.1
根据
\[\frac{h \nu V_{m} W_{i}}{K}=n_{m}
\]
\[K=\frac{h \nu V_{m} W_{i}}{n_{m}}
\]
而\(n_{m}=\frac{I n V_{m}}{c h \nu_{m}}\), 其中\(I\)为光强, 满足8.3-9式,
\[I=\frac{1}{\lambda^{2} g\left(\nu_{0}\right)} 8 \pi h \nu n^{2} t_{自发}W_i
\]
带入得到
\[n_{m}=\frac{n V_{m} W_{i} 8 \pi n^{2} t_{自发} \nu^{2}}{c^{3} g\left(\nu_{0}\right)}
\]
所以得到
\[K=\frac{c^{3} h \nu V_{m} W_{i}}{n V_m W_i 8 \pi n^{2} t\nu^2\Delta \nu}=\frac{h \nu c^{3}}{8 \pi n^{3} \nu^{2} \Delta \nu t}
\]
9.2
由9.1-21式, 当有横向约束时, 内部损耗\(\alpha\)增大, 由
\[\nu=\nu_{m}-\left(\nu-\nu_{0}\right)\frac{c\left[\alpha-1/l \ln\left(r_{1} r_{2}\right)\right]}{2 \pi n \Delta \nu}
\]
可知, 激光共振频率将会稍稍远离无源腔共振频率.
利用9.1-18式,
\[\nu_{m}=\frac{m c}{2 n l}+\frac{c}{2 \pi n l}\left(\tan ^{-1} \frac{z_{2}}{z_{0}}-\tan ^{-1} \frac{z_{1}}{z_{0}}\right)
\]
再利用\(\arctan a-\arctan b=\arctan \frac{a-b}{1+a b}\)可以化简. 对于共焦腔, 利用6.6-13和7.1-10可得\(z_0=l/2\), 所以有
\[\nu_{m}=\frac{m c}{2 n l}+\frac{c}{2 \pi n l} \arctan \frac{l z_{0}}{z_{0}^{2}+z_{1} z_{2}}
\]
利用
\[z_{1}=-\frac{l}{2}, z_{2}=\frac{l}{2}
\]
代入可得
\[\arctan \frac{l z_{0}}{z_{0}^{2}+z_{1} z_{2}}=\arctan \frac{\frac{1}{2} l^{2}}{\frac{1}{4} l^{2}-\frac{1}{4} l^{2}}=\frac{\pi}{2}
\]
所以共焦腔有
\[\nu_{m}=\frac{m c}{2 n l}+\frac{c}{4 n l}
\]
而当\(z_0\gg l\)时, \(\arctan \frac{l z_{0}}{z_{0}^{2}+z_1z_{2}}=0\), 所以,
\[\nu_{m}=\frac{m c}{2 n l}
\]
9.3
在\(\text{F-P}\)腔中, \(\omega_0=\infty\), \(\tan ^{-1} \frac{z_{1}}{z_{0}}=\tan ^{-1} \frac{z_{2}}{z_{0}}=0\), 由9.1-10式, 振荡条件为\(k^{\prime} l=m \pi\),
\[k^{\prime}=k\left[1+\frac{\chi^{\prime}(w)}{2 n^{2}}\right]
\]
所以
\[\omega_{n}=\frac{\pi c m}{ln \left[1+\frac{1}{2 n^{2}} \chi^{\prime}(\omega)\right]}
\]
从而可得
\[m=\frac{ln}{\pi c} \omega_{m}\left[1+\frac{1}{2 n^{2}} x^{\prime}(\omega)\right]
\]
\[m-1=\frac{l n}{\pi c} \omega_{m-1}\left[1+\frac{1}{2 n^{2}}\left(x^{\prime}\left(\omega_{m}\right)+\frac{d \chi(\omega)}{d \omega}\left(\omega_{m-1}-\omega_{m}\right)\right)\right]
\]
两式作差得到
\[\omega_{m}-\omega_{m-1}=\frac{\pi c}{n l\left[1+\frac{\omega}{2 n^{2}} \frac{d \chi(\omega)}{d \omega}\right]_{\omega=\omega_{m}}}
\]
9.4
式9.2-14中, \(\omega_l\)是无源腔的振荡频率, 而\(\omega\)是实际激光频率. 因此实际上\(\omega_l\)对应9.1-17中令\(\chi'=0\)的\(\omega\), 而\(\omega\)则直接就是9.1-17中的\(\omega\). 二者作差得到
\[\omega_{l}-\omega\left[1+\frac{\chi^{\prime}(\nu)}{2 n^{2}}\right]=0
\]
因此
\[\omega_{l}^{2}-\omega^{2} \simeq \omega^{2} \frac{\chi^{\prime}(\nu)}{n^{2}}\tag{$*$}
\]
将9.1-14带入9.1-14a中, 得到
\[e^{\left(- k \frac{\chi^{\prime \prime}(\nu)}{n^{2}}-\alpha\right) \cdot l}=\frac{1}{r_{1} r_{2}}
\]
即
\[\frac{\omega n}{c} \cdot \frac{x^{\prime \prime}(\nu)}{n^{2}}=-\alpha+\frac{1}{l}\ln(r_1r_2)
\]
令
\[\sigma=\left[\alpha-\frac{1}{l} \ln \left(r_{1} r_{2}\right)\right] \frac{c}{n} \cdot \varepsilon
\]
则有
\[\frac{\omega\chi^{\prime \prime}(\nu)}{n^{2}}=-\frac{\sigma}{\varepsilon}
\]
以\((-i)\)乘以上式并加上\((*)\)式可得
\[\omega_{c}^{2}-\omega^{2}+i \frac{\sigma \omega}{\varepsilon}=\omega^{2} \frac{1}{n^{2}}\left(\chi^{\prime}(\nu)-i \chi^{\prime \prime}(\nu)\right)
\]
9.6
稳态时有\(\frac{d}{d t} N_{i}=0\),
\[\left\{\begin{array}{l}{R_{2}-\frac{N_{2}}{t_{1}}-\left(N_{2}-\frac{g_{2}}{g_{1}} N_{1}\right) W_{i}(\nu)=0} \\ {R_{1}-\frac{N_{1}}{t_{1}}+\frac{N_{2}}{t_{21}}+\left(N_{2}-\frac{g_{2}}{g_{1}} N_{1}\right) W_{i}(\nu)=0}\end{array}\right.
\]
得到
\[\left\{\begin{array}{l}{N_{1}=\frac{\left(\frac{1}{t_{2}}+W_{i}\right) N_{2}-R_{2}}{\frac{g_{2}}{g_{1}} W_{i}}} \\ {N_{2}=\frac{t_{2} R_{2}+\left(R_{1}+R_{2}\right) t_{1}t_2\frac{g_{2}}{g_{1}} W_{i}}{1+W_{i}\left[t_{2}+(1-\delta) \frac{g_{2}}{g_{1}}\right]}}\end{array}\right.
\]
所以
\[\Delta N \equiv N_{2}-\frac{g_{2}}{g_{1}} N_{1}=\frac{R_{2} t_{2}-\left(R_{1}+\delta R_{2}\right) t_{1} \frac{g_{2}}{g_{1}}}{1+\left[t_{2}+(1-\delta) t_{1} \frac{g_{2}}{g_{1}}\right] W_{i}(\nu)}
\]
